Inside the Black Box: 5 Methods for Explainable AI (XAI)
by Murat Durmus
Explainable artificial intelligence (XAI) is the attempt to make the finding of results of non-linearly programmed systems transparent to avoid so-called black-box processes. The main task of XAI is to make non-linear programmed systems transparent. It offers practical methods to explain AI models, which, for example, correspond to the regulation of the data protection laws of the European Union (DSVGO).

The following five methods are listed, which have to make AI models more transparent and understandable.
1. Layer-wise relevance propagation (LRP)
Layer-wise Relevance Propagation (LRP) is a technique that brings such explainability and scales to potentially highly complex deep neural networks. It operates by propagating the prediction backward in the neural network, using a set of purposely designed propagation rules.
Source & more info: https://link.springer.com/chapter/10.1007/978-3-030-28954-6_10
2. Counterfactual method
The method of counterfactual impact evaluation allows to identify which part of the observed actual improvement (e.g. increase in income) is attributable to the impact of the intervention (since such improvement might occur not only due to the intervention but also due to other factors, e.g. overall economic growth).
Source & more info: http://www.bgiconsulting.lt/counterfactual-analysis
3. Local interpretable model-agnostic explanations (LIME)
Lime is short for Local Interpretable Model-Agnostic Explanations. Each part of the name reflects something that we desire in explanations. Local refers to local fidelity – i.e., we want the explanation to really reflect the behavior of the classifier “around” the instance being predicted.
Source & more info: https://homes.cs.washington.edu/~marcotcr/blog/lime/
4. Generalized additive model (GAM)
In statistics, a generalized additive model (GAM) is a generalized linear model in which the linear predictor depends linearly on unknown smooth functions of some predictor variables, and interest focuses on inference about these smooth functions. GAMs were originally developed by Trevor Hastie and Robert Tibshirani to blend properties of generalized linear models with additive models.
The model relates a univariate response variable, Y, to some predictor variables, xi. An exponential family distribution is specified for Y (for example normal, binomial or Poisson distributions) along with a link function g (for example the identity or log functions) relating the expected value of Y to the predictor variables via a structure such as
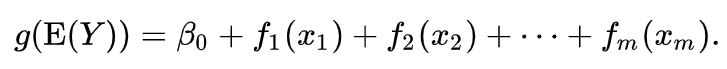
The functions fi may be functions with a specified parametric form (for example a polynomial, or an un-penalized regression spline of a variable) or may be specified non-parametrically, or semi-parametrically, simply as ‘smooth functions’, to be estimated by non-parametric means. So a typical GAM might use a scatterplot smoothing function, such as a locally weighted mean, for f1(x1), and then use a factor model for f2(x2). This flexibility to allow non-parametric fits with relaxed assumptions on the actual relationship between response and predictor, provides the potential for better fits to data than purely parametric models, but arguably with some loss of interpretability.
Source & more info: https://en.wikipedia.org/wiki/Generalized_additive_model
5. Rationalization
AI rationalization, an approach for generating explanations of autonomous system behavior as if a human had performed the behavior. We describe a rationalization technique that uses neural machine translation to translate internal state-action representations of an autonomous agent into natural language. We evaluate our technique in the Frogger game environment, training an autonomous game playing agent to rationalize its action choices using natural language. A natural language training corpus is collected from human players thinking out loud as they play the game. We motivate the use of rationalization as an approach to explanation generation and show the results of two experiments evaluating the effectiveness of rationalization. Results of these evaluations show that neural machine translation is able to accurately generate rationalizations that describe agent behavior, and that rationalizations are more satisfying to humans than other alternative methods of explanation.
Source & more info: https://arxiv.org/pdf/1702.07826.pdf

Thanks for your attention. I hope you enjoyed the brief overview.
Murat
(Author of the Book: THE AI THOUGHT BOOK)