The more statistical techniques a Data Scientist has mastered, the better the results can be. In this blog article, we want to introduce you to ten common techniques that should not be missing in the repertoire of a data scientist.
[bctt tweet=”10 Statistical Techniques Data Scientists Should Master #AI #ML #KI #DataScience #statistics #machinelearning #analytics #BigDataAnalytics #BI #Algorithms” username=”AISOMA_AG”]
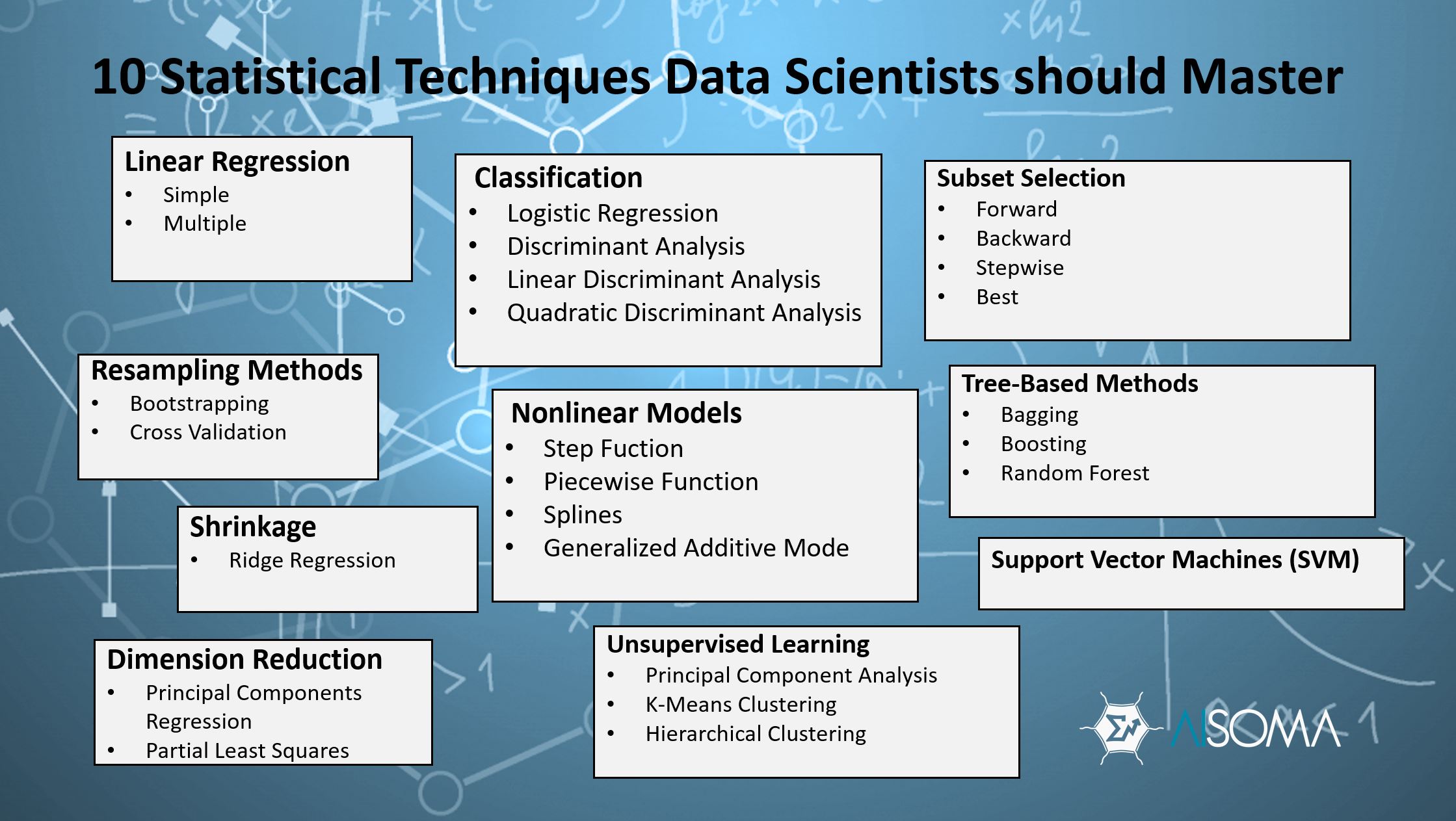
10 Statistical Techniques for Data Scientists

1. Linear Regression
In statistics, linear regression is a linear approach to modeling the relationship between a scalar response (or dependent variable) and one or more explanatory variables (or independent variables). The case of one explanatory variable is called simple linear regression. For more than one explanatory variable, the process is called multiple linear regression. This term is distinct from multivariate linear regression, where multiple correlated dependent variables are predicted, rather than a single scalar variable. (more info: Wikipedia)
2. Classification
In machine learning and statistics, classification is the problem of identifying to which of a set of categories (sub-populations) a new observation belongs, on the basis of a training set of data containing observations (or instances) whose category membership is known. Examples are assigning a given email to the “spam” or “non-spam” class, and assigning a diagnosis to a given patient based on observed characteristics of the patient (sex, blood pressure, presence or absence of certain symptoms, etc.). Classification is an example of pattern recognition. (more info: Wikipedia)
3. Resampling
In statistics, resampling is any of a variety of methods for doing one of the following:
- Estimating the precision of sample statistics (medians, variances, percentiles) by using subsets of available data (jackknifing) or drawing randomly with replacement from a set of data points (bootstrapping)
- Exchanging labels on data points when performing significance tests (permutation tests, also called exact tests, randomization tests, or re-randomization tests)
- Validating models by using random subsets (bootstrapping, cross-validation)
(more info: Wikipedia)
4. Shrinkage
In statistics, shrinkage has two meanings:
- In relation to the general observation that, in regression analysis, a fitted relationship appears to perform less well on a new data set than on the data set used for fitting. In particular the value of the coefficient of determination ‘shrinks’. This idea is complementary to overfitting and, separately, to the standard adjustment made in the coefficient of determination to compensate for the subjunctive effects of further sampling, like controlling for the potential of new explanatory terms improving the model by chance: that is, the adjustment formula itself provides “shrinkage.” But the adjustment formula yields an artificial shrinkage, in contrast to the first definition.
- To describe general types of estimators, or the effects of some types of estimation, whereby a naive or raw estimate is improved by combining it with other information (see shrinkage estimator). The term relates to the notion that the improved estimate is at a reduced distance from the value supplied by the ‘other information’ than is the raw estimate. In this sense, shrinkage is used to regularize ill-posed inference problems.
(more info: Wikipedia)
5. Dimension Reduction
In statistics, machine learning, and information theory, dimensionality reduction or dimension reduction is the process of reducing the number of random variables under consideration by obtaining a set of principal variables. It can be divided into feature selection and feature extraction.
(more info: Wikipedia)
6. Nonlinear Models
The rapid and sustained increases in computing power starting from the second half of the 20th century have had a substantial impact on the practice of statistical science. Early statistical models were almost always from the class of linear models, but powerful computers, coupled with suitable numerical algorithms, caused an increased interest in nonlinear models (such as neural networks) as well as the creation of new types, such as generalized linear models and multilevel models.
(more info: Wikipedia)
7. Unsupervised Learning
Unsupervised learning is a branch of machine learning that learns from test data that has not been labeled, classified or categorized. Instead of responding to feedback, unsupervised learning identifies commonalities in the data and reacts based on the presence or absence of such commonalities in each new piece of data. Alternatives include supervised learning and reinforcement learning.
(more info: Wikipedia)
8. Support Vector Machine (SVM)
In machine learning, support-vector machines (SVMs, also support-vector networks) are supervised learning models with associated learning algorithms that analyze data used for classification and regression analysis. Given a set of training examples, each marked as belonging to one or the other of two categories, an SVM training algorithm builds a model that assigns new examples to one category or the other, making it a non-probabilistic binary linear classifier (although methods such as Platt scaling exist to use SVM in a probabilistic classification setting).
An SVM model is a representation of the examples as points in space, mapped so that the examples of the separate categories are divided by a clear gap that is as wide as possible. New examples are then mapped into that same space and predicted to belong to a category based on which side of the gap they fall.
(more info: Wikipedia)
9. Subset Selection
n machine learning and statistics, feature selection, also known as variable selection, attribute selection or variable subset selection, is the process of selecting a subset of relevant features (variables, predictors) for use in model construction. Feature selection techniques are used for four reasons:
- simplification of models to make them easier to interpret by researchers/users,
- shorter training times,
- to avoid the curse of dimensionality,
- enhanced generalization by reducing overfitting (formally, reduction of variance)
The central premise when using a feature selection technique is that the data contains some features that are either redundant or irrelevant and can thus be removed without incurring much loss of information. Redundant and irrelevant are two distinct notions, since one relevant feature may be redundant in the presence of another relevant feature with which it is strongly correlated.
(more info: Wikipedia)
10. Tree-Based Methods
In computer science, Decision tree learning uses a decision tree (as a predictive model) to go from observations about an item (represented in the branches) to conclusions about the item’s target value (represented in the leaves). It is one of the predictive modeling approaches used in statistics, data mining and machine learning. Tree models where the target variable can take a discrete set of values are called classification trees; in these tree structures, leaves represent class labels and branches represent conjunctions of features that lead to those class labels. Decision trees where the target variable can take continuous values (typically real numbers) are called regression trees.
(more info: Wikipedia)

[bctt tweet=”10 Statistical Techniques Data Scientists Should Master #AI #ML #KI #DataScience #statistics #machinelearning #analytics #BigDataAnalytics #BI #Algorithms” username=”AISOMA_AG”]
Further readings: